Recently I’ve been shipping frozen vials of cells to collaborators. The standard packaging for such shipments looks like this:
This got me wondering: how thick should the Styrofoam insulation be, in order to maximize the time before the dry ice is gone? Thicker insulation is better for blocking heat, but allows less room to add dry ice.
I. Assumptions
To make things solvable, let’s make the following assumptions about the problem:
The volume of the vials of cells is negligible compared to the box volume.
The box is actually a sphere. We will denote the outer radius as R.
The outside surface of the insulation is fixed at 30 °C.
The inside surface of the insulation is fixed at –78 °C (the sublimation temperature of dry ice), at least until all the dry ice sublimates.
II. Heat flow through the insulation
First, we need to find the heat flow through the shell of insulation. We consider an infinitesimal section of the shell at radius r. The heat flow Q into this section is given by Fourier’s law:
Separating variables and integrating:
Solving the integrals:
Rearranging for the solution:
Note that because R > r, the heat flow is negative when ∆T is positive. This is because heat flows in the opposite direction of a temperature gradient.
III. Heat required to sublimate the dry ice
The enthalpy of sublimation of solid carbon dioxide is about 26 kJ/mol, and the molecular weight is 44 g/mol. So:
IV. Time required to sublimate the dry ice
The time required (in seconds) is equal to the heat required (in joules) divided by the heat flow (in watts). So:1
Rearranging, and collapsing everything that doesn’t involve r into a constant K:
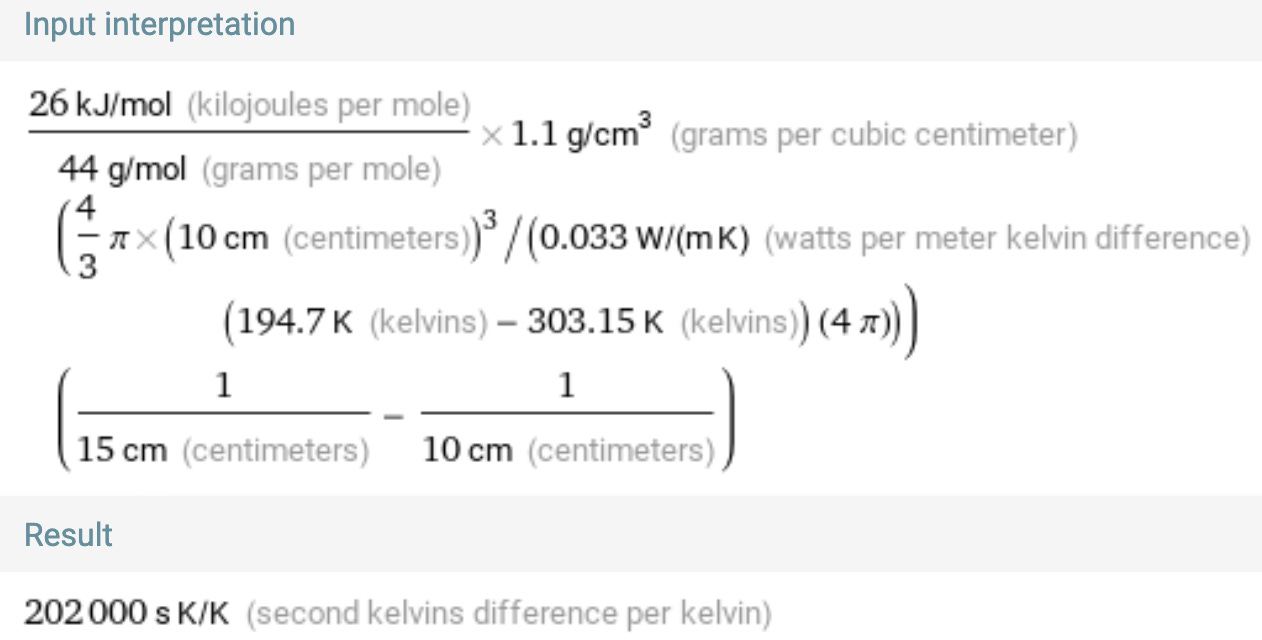
Let’s do a quick sanity check (plugging in some known values) and see if the result makes sense. We’ll do a 10 cm radius sphere of dry ice packed at 1.1 g/cm3,2 surrounded by an additional 5 cm of Styrofoam (heat conductivity 0.033 W/m*K).
Putting everything into Wolfram Alpha gives a result of 202,000 seconds, or about 56 hours. This seems quite reasonable, actually!
V. Maximization
Now we need to take the derivative and set it to zero:
This has two solutions:
r = 0 (corresponding to no dry ice, a minimum time)
r = 2/3 R (corresponding to the maximum time)
So, the overall solution to our problem says that the radius of dry ice should be 2/3 the radius of the overall container.
VI. Does this make sense?
Interestingly, the choice of r does not depend at all on the type of insulation or the type of cryogen! Even if your “insulation” is a very good heat conductor, this result implies that you should still use quite a lot of it.
And here we can see one of our assumptions failing. This model assumes that the heat flow will be infinite if there is no insulation.3 In reality, the heat transfer between the environment and the surface of the box will take place through a boundary layer of air. If the “insulator” is not a good insulator, or the insulation is very thin, then the heat flow in the model will be much larger than it will be in real life.
However, for the kinds of packages I am considering, even when they are packed with dry ice, they are not cold to the touch, implying that the surface temperature is nearly equal to the ambient temperature. So, I think this assumption is still reasonable in this case (but not in others).
Another assumption that’s not quite right is that we have boxes that are cubes, not spheres. A cube has a larger surface area per volume than a sphere, so the heat flow will be higher. But I think this will just go into the constant term, and the factor of 2/3 will still be the same.
VII. Exercises for the reader
How does including surface heat transfer coefficients change this result?
What if the volume of the product to be shipped is not negligible compared to the package volume?
Most Styrofoam coolers that I’ve seen have their insulation thinner than 1/3 of the total radius. Why?4
A space mission is launching a camera that needs to be kept cool on the surface of Venus. The total mass available for insulation and coolant is 100 kg. What is the longest possible time that can be obtained before the camera overheats?
I am not 100% sure that I didn’t introduce an incorrect sign change somewhere along the way, but for the final result this doesn’t matter.
The density of solid CO2 is 1.56 g/cm3 but I am assuming a ~70% packing density for dry ice granules.
This is a consequence of assuming a fixed temperature at the surfaces.
My best guess is that they want to have additional volume for packing larger objects.











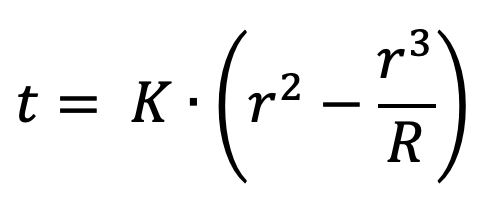


@exercise 3: Unless I'm very much mistaken, these boxes are meant for transportation, not storage. So duration of cooling is a *constraint*, not a *goal* in their design. They just need to keep the content cold until it can be transferred to actively cooled storage or used, not as long as possible.
Thus, you use just enough insulation to satisfy the constraint and optimize for other goals, like material cost and space efficiency.
This is what Substack needs! Really good.